AWS 기술 블로그
양자 컴퓨팅이란 무엇인가? – Part 4: 양자 컴퓨터가 빠르다는 의미, 양자 회로, 양자 연산의 원리
이번 블로그는 ‘양자 컴퓨팅이란 무엇인가?’ 시리즈의 네 번째 글로, 양자 컴퓨터의 속도와 양자 회로에 대해 심층적으로 알아봅니다.
시리즈 블로그 보기
- 양자 컴퓨팅이란 무엇인가? – Part 1: 양자 컴퓨터의 개념, 등장 배경, 분류 체계 등
- 양자 컴퓨팅이란 무엇인가? – Part 2: 양자 컴퓨터가 적합한 문제들, 활약이 기대되는 분야, 양자 컴퓨터 생태계
- 양자 컴퓨팅이란 무엇인가? – Part 3: 큐비트, 양자 중첩, 얽힘 및 측정, 고속 연산을 수행하는 방법
- 양자 컴퓨팅이란 무엇인가? – Part 4: 양자 컴퓨터가 빠르다는 의미, 양자 회로, 양자 연산의 원리
- 양자 컴퓨팅이란 무엇인가? – Part 5: QPU
- 양자 컴퓨팅이란 무엇인가? – Part 6: 양자 컴퓨터의 성능지표, 도전 사항, 양자 오류 제어
- 양자 컴퓨팅이란 무엇인가? – Part 7: 하이브리드 접근법, 양자 연산이 구현되는 여정
양자 컴퓨터가 고전 컴퓨터보다 빠르다는 말은 종종 오해를 불러일으킵니다. 실제로 양자 컴퓨터의 진정한 강점은 개별 연산 속도가 아니라, 양자 중첩과 얽힘을 통해 문제의 크기가 커질수록 총계산 횟수를 획기적으로 줄일 수 있다는 점에 있습니다. 이번 글에서는 양자 컴퓨터의 속도가 갖는 진정한 의미를 살펴보고, 큐비트를 조작하여 양자 연산을 수행하는 양자 회로의 개념과 특성, 그리고 양자 연산의 원리에 대해 알아보겠습니다. 파동과 간섭 현상을 기반으로 하는 양자 컴퓨팅의 독특한 계산 방식이 어떻게 기존 컴퓨터와 차별화되는지 알아보도록 하겠습니다.
양자 컴퓨터가 빠르다는 의미
양자 컴퓨터가 고전 컴퓨터보다 항상 빠르다고 말하는 것은 오해의 소지가 있습니다. 실제로 양자 컴퓨터가 모든 상황에서 고전 컴퓨터를 능가하는 것은 아니며, 그 속도 우위는 특정 조건에서만 나타납니다. 일반적으로 연산에 드는 총시간은 그림1과 같이 1회당 계산 시간과 총계산 횟수의 곱으로 나타낼 수 있는데, 양자 컴퓨터의 가장 큰 장점은 지난 블로그에서 설명한 것처럼, 중첩과 얽힘과 같은 양자 역학적 현상을 이용해 총계산 횟수를 획기적으로 줄일 수 있다는 점입니다. 즉, 문제의 크기가 커지더라도 고전 컴퓨터처럼 계산 횟수가 기하급수적으로 증가하지 않고, 효율적으로 연산을 처리할 수 있습니다.
따라서 양자 컴퓨터가 진정한 속도 우위를 보이기 위해서는 문제의 크기가 충분히 커져야 하며, 양자 컴퓨터의 계산 시간은 문제 크기가 커질수록 고전 컴퓨터에 비해 더 느리게 증가하기 때문에 아주 큰 문제에서만 양자 가속 효과가 실질적으로 나타납니다.
또한, 개별 연산 속도 측면에서는 양자 컴퓨터가 항상 고전 컴퓨터보다 빠르다고 할 수 없습니다. 현재의 양자 컴퓨터는 하드웨어의 한계와 오류 수정에 따른 오버헤드 등 여러 기술적 제약으로 인해, 한 번의 연산 속도 자체도 고전 컴퓨터보다 느린 경우가 많습니다. 고전 컴퓨터는 오랜 시간에 걸쳐 기술이 발전해 매우 빠른 연산 속도를 자랑합니다.
양자 컴퓨터가 빠르다고 하는 것은, 결국 개별 연산의 속도보다는 복잡도가 높은 특정 문제에서 총계산 횟수를 대폭 줄일 수 있다는 데에 그 의미가 있습니다. 양자 컴퓨터의 속도 우위는 중첩과 얽힘 등 양자 역학적 특성을 활용할 수 있는 문제에만 나타나며, 그렇지 않으면 오히려 고전 컴퓨터가 더 효율적일 수 있다는 점을 반드시 염두에 두어야 합니다.
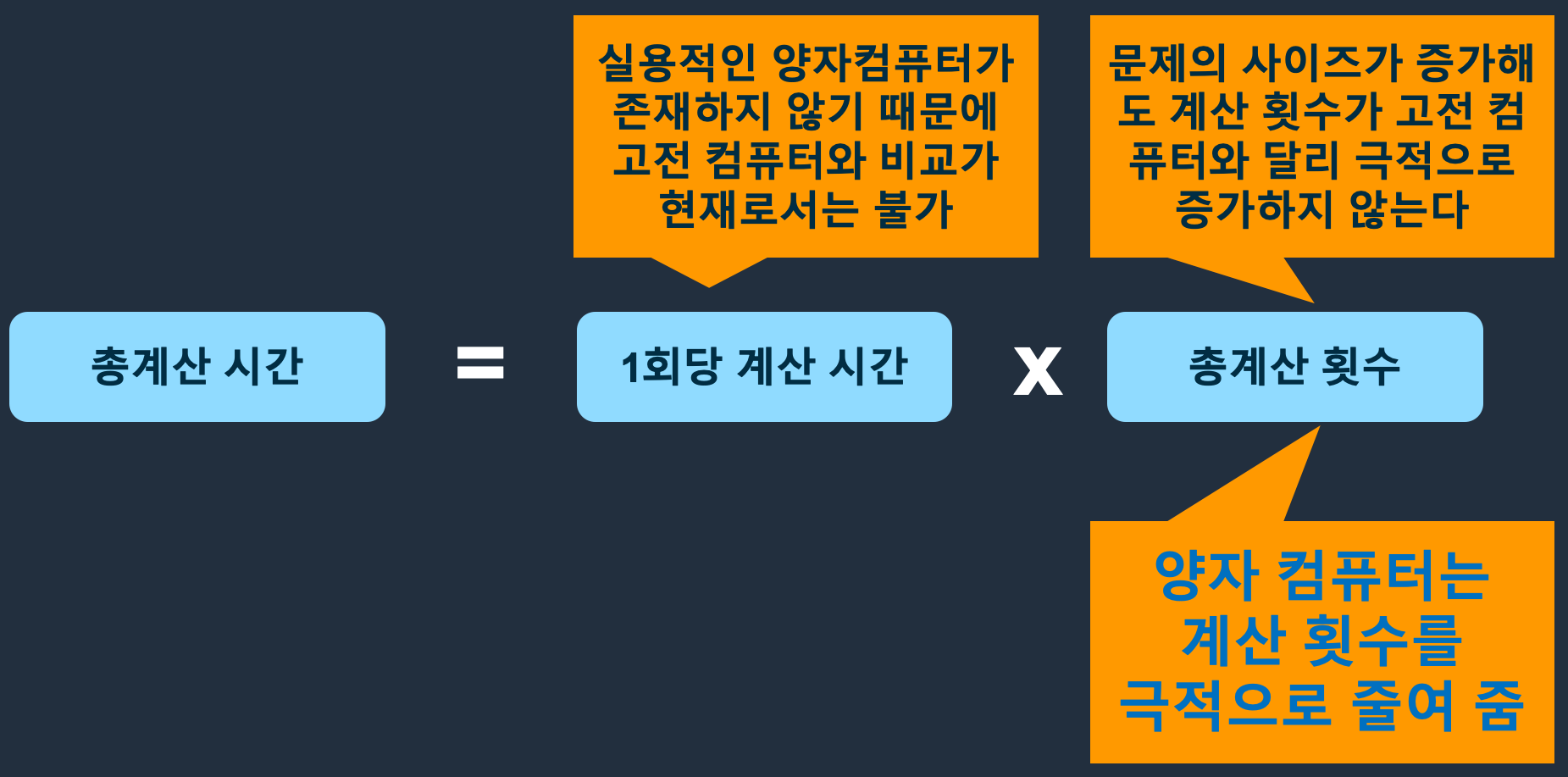
그림 1. 양자 컴퓨터가 빠르다는 의미의 개념
큐비트를 조작하여 양자 연산(중첩, 얽힘 및 간섭)을 수행하는 양자 회로
다음은 큐비트를 조작하여 양자 연산을 수행하는 양자 회로에 대해 알아보도록 하겠습니다. 우선 자세한 내용에 대한 소개에 앞서, 그림2와 같이 양자 컴퓨터 연산 과정에 대해 알아보도록 하겠습니다. 이 예에서는 2개의 큐비트를 포함하는 간단한 양자 컴퓨터 연산 과정을 다루고 있습니다. 연산 과정은 다음과 같이 크게 3단계로 구분할 수 있습니다.
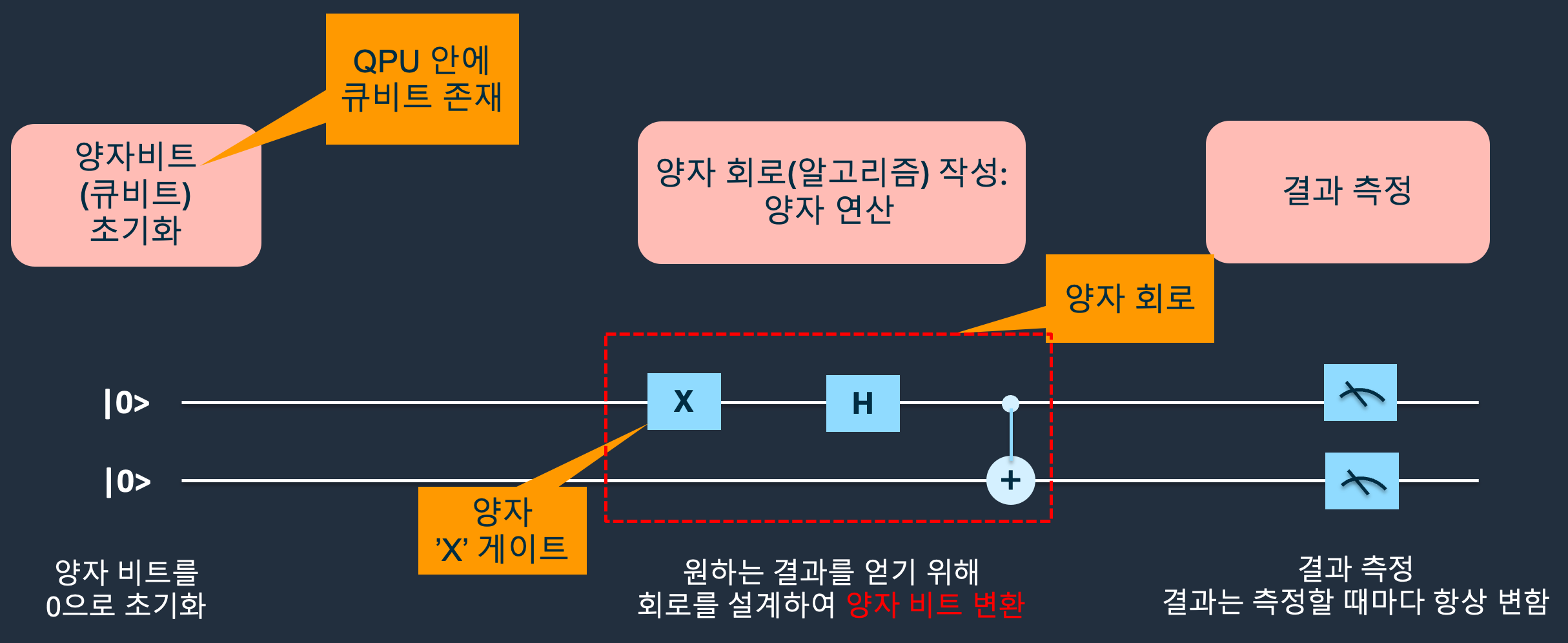
그림 2. 2개의 큐비트를 포함하는 양자 컴퓨터 연산 과정
- 큐비트 초기화: 그림의 맨 왼쪽을 보면, 두 개의 큐비트가 모두 |0⟩ 상태로 시작합니다. 일반적으로 양자 연산에서는 모든 큐비트를 |0⟩ 상태로 초기화합니다. 이 큐비트들은 QPU(Quantum Processing Unit)라는 양자 연산 장치 안에 존재합니다. QPU는 양자 컴퓨터의 두뇌 역할을 합니다.
- 양자 회로 설계 및 연산: 원하는 결과를 얻기 위해, 양자 회로(quantum circuit)를 이용하여 큐비트에 다양한 연산을 적용합니다. 그림2에서 양자 회로는 다수의 양자 게이트(quantum gate)로 구성되어 있음을 확인할 수 있습니다.
- 결과 측정: 양자 회로를 거친 큐비트들은 마지막에 측정이라는 과정을 거칩니다. 이때 큐비트의 상태가 확정되어 0이나 1로 바뀌게 되고, 이 결과가 우리가 실제로 얻는 답입니다. 중요한 점은, 양자 컴퓨터에서는 같은 회로라도 측정할 때마다 결과가 달라질 수 있다는 점입니다. 이는 지난 세 번째 블로그에서 언급한 것처럼, 양자 역학의 확률적 특성 때문입니다.
양자 회로와 양자 게이트는 양자 컴퓨팅의 핵심 요소로, 고전 컴퓨터의 논리 회로와 논리 게이트에 대응하는 개념입니다. 양자 게이트는 단일 큐비트나 다중 큐비트에 작용하는 양자 연산을 의미합니다. 표1은 대표적으로 많이 사용되는 양자 게이트의 예시이며, 실제로는 다양한 양자 게이트가 존재합니다.
| 게이트 | 행렬 표현 | 설명 | 적용 큐비트 |
|---|---|---|---|
| 파울리-X(Pauli-X) | 큐비트 반전(0<->1) | 단일 큐비트 | |
| 하다마드(Hadamard) | 중첩 상태 생성 | 단일 큐비트 | |
| CNOT | 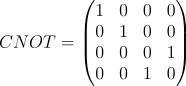 |
조건부 반전 | 2 큐비트 |
<표1. 대표적으로 많이 사용되는 양자 게이트 예시>
표1의 파울리-X 게이트는 큐비트의 0과 1 상태를 서로 반전시키는 역할을 하는, 일종의 Not 게이트 역할을 수행합니다. 하다마드(Hadamard) 게이트는 큐비트를 0과 1이 동시에 존재하는 중첩 상태로 변환합니다. 예를 들어, |0> 상태에 하다마드 게이트를 적용하면 그림3과 같이, 0 상태와 1 상태가 각기 50%씩 존재하는 양자 중첩을 구현할 수 있습니다. CNOT 게이트는 두 개의 큐비트에 적용되며, 제어 큐비트가 1일 때 대상 큐비트를 반전시키는 조건부 연산을 수행합니다. 양자 중첩 상태에, 표1의 CNOT 게이트를 적용하면 양자 얽힘 상태를 구현할 수 있습니다.

그림 3. 하다마드 게이트를 이용한 양자 중첩의 수학적 표현
표2에서 우리가 현재 사용하고 있는 디지털 논리 게이트와 양자 게이트와의 차이점을 정리하였습니다. 이러한 특성은 고전 컴퓨터와 양자 컴퓨터의 본질적 차이를 보여주는 중요한 요소입니다. 디지털 논리 게이트는 대부분 비가역적이며, 연산 과정에서 정보 손실이 발생할 수 있습니다. 반면, 양자 게이트는 모두 가역적이며, 연산 과정에서 정보 손실이 없습니다. 디지털 게이트는 입력과 출력 비트 수가 다를 수 있지만, 양자 게이트는 입력과 출력 큐비트 수가 항상 동일합니다. 또한, 디지털 논리 게이트는 진리표로 표현되고, 0과 1의 이진값만 다룰 수 있지만, 양자 게이트는 유니터리 행렬(Unitary matrix)로 표현되며, 큐비트의 중첩 상태와 얽힘 상태까지 다룰 수 있습니다.
| 항목 | 디지털 논리 게이트 | 양자 게이트 |
|---|---|---|
| 가역성 | 대부분 비가역적 | 모든 게이트가 가역적 |
| 정보 손실 | 연산 과정에서 정보 손실 발생 | 정보 손실 없음 |
| 입출력 관계 | 입력과 출력 비트 수가 다를 수 있음 | 입력과 출력 큐비트 수가 동일 |
| 수학적 표현 | 진리표로 표현 | 유니터리 행렬로 표현 |
| 상태 표현 | 0과 1의 이진값만 가능 | 중첩 상태와 얽힘 상태 가능 |
| 기본 단위 | 비트 | 큐비트 |
| 구현 방식 | 전기 회로로 구현 | 양자 시스템으로 구현 |
| 연산 특성 | 결정론적 결과 | 확률적 결과 |
<표2. 디지털 논리 게이트와 양자 게이트의 차이>
양자 알고리즘, 예를 들어 쇼어 알고리즘(Shor’s algorithm)이나 그로버 알고리즘(Grover’s algorithm)은 간섭 현상을 정밀하게 설계하여 특정 해답의 확률을 증폭하는 구조로 만들어집니다. 이러한 간섭 현상은 양자 회로(Quantum Circuit)를 통해 실제로 구현되며, 양자 회로는 다양한 양자 게이트를 시간 순서에 따라 배열하여 큐비트의 상태와 위상을 조절함으로써, 추상적인 알고리즘을 실제 하드웨어에서 실행 가능한 형태로 변환합니다.
즉, 양자 회로는 원하는 간섭 패턴을 만들어내기 위한 구체적인 도구로, 알고리즘의 설계에 따라 특정 해답의 확률을 높이고 나머지 해답의 확률은 억제하는 역할을 합니다. 큐비트는 고전적 비트와 달리 중첩(superposition) 상태에 있을 수 있고, 양자 게이트는 큐비트의 확률 진폭과 위상을 변화시켜 연산을 수행합니다. 이러한 양자 회로는 고전 논리 회로와 유사한 구조를 가지면서도, 중첩, 간섭, 얽힘 등 양자역학적 특성을 적극적으로 활용한다는 점에서 차별화되며, 이로 인해 고전 회로로는 불가능한 계산 효율성과 정보 처리 방식을 실현할 수 있습니다.
양자 회로의 가장 중요한 특징은 앞서 언급한 가역성입니다. 이는 회로에서 측정하기 전까지 모든 양자 연산을 역순으로 되돌릴 수 있다는 뜻으로, 중간 과정에서 정보가 전혀 사라지지 않음을 의미합니다. 고전 컴퓨터에서는 연산 과정에서 가역성이 보장되지 않습니다. 즉, 입력 비트가 출력으로 변환되는 과정에서 비트의 개수가 줄어들거나, 일부 정보가 소실되기도 합니다. 이로 인해 출력 정보만으로는 원래의 입력 상태를 정확하게 추정하기 어렵고, 정보가 사라지는 과정에서 열이 발생합니다. 이러한 현상은 ‘란다우어의 법칙(Landauer’s Principle)’로 설명되며, 실제로 CPU나 데이터센터에서 많은 열이 발생하는 근본적인 원인이 됩니다. 반면, 양자 컴퓨터에서는 입력과 출력의 큐비트 개수가 항상 동일하게 유지됩니다. 양자 회로를 구성하는 모든 연산(양자 게이트)은 유니터리 연산으로, 본질적으로 가역적입니다. 즉, 양자 회로에서 연산이 진행되는 동안 정보가 소실되지 않으며, 이론적으로 모든 연산 과정을 역순으로 되돌려 원래의 입력 상태로 복원할 수 있습니다. 이러한 가역성 덕분에 양자 컴퓨터는 연산 과정에서 열 발생이 거의 없고, 에너지 소비도 매우 적습니다.
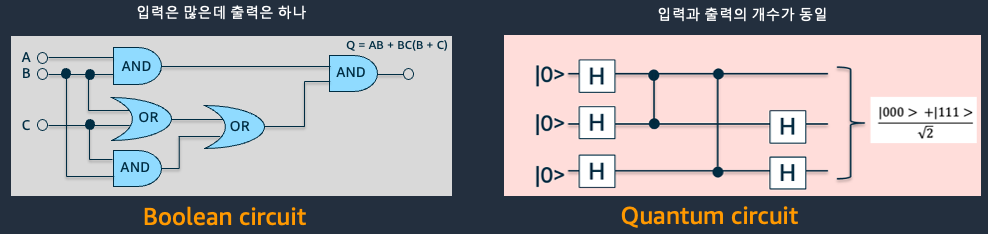
그림 4. 디지털 회로와 양자 회로의 비교
또 하나의 특징은 결과의 확률성입니다. 동일한 입력값을 가지고 같은 양자 회로를 여러 번 실행해도, 측정 결과가 매번 다르게 나올 수 있습니다. 이는 양자 상태가 중첩되어 있기 때문에, 측정할 때마다 확률에 따라 결과가 정해지기 때문입니다.
결론적으로 이야기하자면, 양자 회로는 양자 알고리즘을 실제로 구현하는 구체적인 도구입니다. 양자 알고리즘이 문제를 해결하기 위한 추상적인 절차와 수학적 아이디어를 담고 있다면, 양자 회로는 이를 실제 큐비트와 게이트를 이용해 실행하는 방법을 제시합니다. 예를 들어, 소인수분해 문제를 푸는 쇼어 알고리즘은 추상적인 개념에 불과하지만, 실제로 이를 구현하려면 어떤 게이트를 어떤 순서로, 어떤 큐비트에 적용할지 구체적으로 설계해야 합니다. 바로 이 역할을 하는 것이 양자 회로입니다.
양자 회로 설계 방법
그렇다면 실제로 양자 회로를 설계하는 방법에 대해 알아보도록 하겠습니다. 양자 컴퓨팅은 기존 컴퓨팅과 근본적으로 다른 패러다임을 요구합니다. 큐비트는 중첩과 얽힘 같은 양자역학적 특성을 활용하며, 확률적 결과를 다룹니다. 양자 프로그래밍 프레임워크는 이러한 복잡한 양자역학적 개념을 추상화하고, 개발자가 양자 하드웨어의 세부사항을 이해하지 않고도 양자 알고리즘을 설계하고 실행할 수 있게 해줍니다. 현재 양자 컴퓨팅 분야에서는 다양한 기업들이 자체 프로그래밍 프레임워크를 개발하여 제공하고 있습니다. AWS는 Amazon Braket SDK를, IBM은 Qiskit을, Microsoft는 Quantum Development Kit(QDK)를, Rigetti는 Forest를, Google은 Cirq를 각각 자사의 양자 프로그래밍 프레임워크로 제공하고 있습니다.
| Company | 양자 프로그래밍 프레임워크 | 지원 프로그래밍 언어 |
|---|---|---|
| AWS | Amazon Braket SDK | Python |
| IBM | Qiskit | Python |
| Microsoft | Quantum Development Kit (QDK) | Q# |
| Rigetti | Forest | Python |
| Cirq | Python |
<표3. 양자 프로그래밍의 대표적인 예시>
흥미로운 점은 IBM, Google, Amazon 등 주요 기업들이 파이썬(Python)을 양자 프로그래밍의 주된 언어로 채택하고 있다는 것입니다. 파이썬은 직관적인 문법과 풍부한 라이브러리 덕분에 양자 알고리즘 개발에 매우 적합한 환경을 제공합니다. 한편, Microsoft는 Q#이라는 독립적인 양자 프로그래밍 언어를 제공하고 있습니다. Q#은 C#과 유사한 문법을 갖고 있지만, 실제로는 C#의 확장판이 아니라 양자 컴퓨팅에 특화된 별도의 언어입니다. Q#은 Python과 연동해 사용할 수도 있습니다. 따라서 양자 프로그래밍을 시작하려는 개발자라면, 다양한 플랫폼에 접근하기 위해 파이썬을 익히는 것이 가장 실용적이라고 할 수 있습니다.
아래 코드는 AWS에서 제공하는 양자 컴퓨팅 서비스인 Amazon Braket을 사용하여 간단한 양자 회로를 생성하고 실행하는 과정을 보여줍니다. 코드의 상세 내용과 실행 결과에 대해서는 별도의 블로그에서 더 자세히 설명하도록 하겠습니다.
import numpy as np
import matplotlib.pyplot as plt
from braket.aws import AwsDevice
# 디바이스(시뮬레이터) 선택
device = AwsDevice("arn:aws:braket:::device/quantum-simulator/amazon/sv1")
#양자 회로 정의
bell = Circuit().h(0).cnot(control=0, target=1)
# 양자 회로 실행(측정)
result = device.run(bell, shots=1000).result()
# 실행 결과 저장
counts = result.measurement_counts양자 연산의 원리
양자 컴퓨터는 우리가 익숙한 일반 컴퓨터와는 근본적으로 다른 원리로 작동합니다. 세 번째 블로그에서 언급한 것처럼, 양자 컴퓨팅의 핵심은 ‘파동’과 ‘간섭’ 현상에 있습니다. 일반 컴퓨터가 0과 1이라는 명확한 상태만을 다루지만, 양자 컴퓨터는 파동의 특성을 활용하여 정보를 처리합니다. 양자 정보는 물결 모양의 파동 패턴으로 표현되며, 이는 여러 가능성을 동시에 담고 있습니다.
양자 계산에서 가장 중요한 메커니즘은 파동의 간섭 현상입니다. 이 간섭에는 보강과 상쇄라는 두 가지 유형이 존재합니다. 보강 간섭은 파동이 서로 만나 더 강해지는 현상으로, 마치 두 물결이 만나 더 높은 파도를 형성하는 것과 유사합니다. 반면 상쇄 간섭은 파동이 서로 만나 약해지거나 소멸하는 현상으로, 두 물결이 만나 서로를 상쇄시켜 잔잔해지거나 소멸하는 것과 유사합니다.
그림5는 양자 컴퓨터의 계산 방식을 시각적으로 보여줍니다. 그림과 같이 만약 3개의 큐비트가 |0>으로 초기화 되어있을 때, 양자 컴퓨터는 8가지 패턴(000~111)을 모두 동시에 처리할 수 있는데, 이것이 바로 양자 컴퓨터의 놀라운 병렬 처리 능력입니다. 이 파동 패턴들은 양자 회로를 통과하면서 변화하며, 각 게이트(사각형과 원 기호)는 파동을 특정 방식으로 변형시킵니다.
양자 회로 설계의 핵심은 “보강 및 상쇄 간섭으로 정답에 해당하는 상태의 확률 진폭만 잘 증가시키고, 오답에 해당하는 상태의 확률 진폭은 제거하는 방식”입니다. 이미지에서 회색으로 강조된 경로가, 바로 이러한 증폭되는 목표 상태를 나타냅니다. 모든 계산이 끝나면 “측정”이라는 과정을 통해 하나의 결과가 선택되며, 이때 증폭된 상태(정답)가 높은 확률로 선택됩니다.
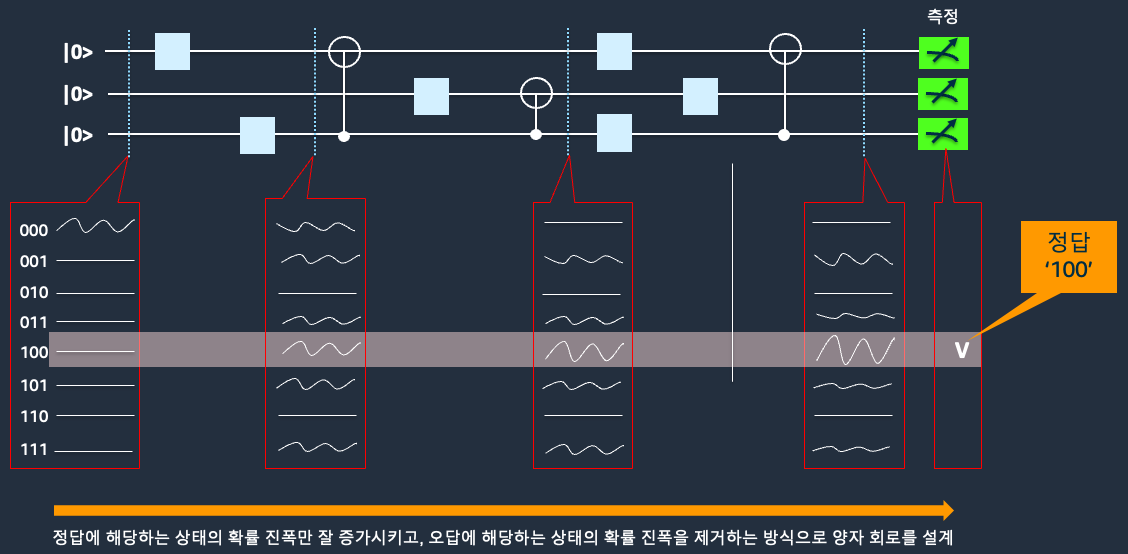
그림 5. 양자 컴퓨터가 계산하는 방법
이를 쉽게 비유하자면, 양자 계산은 여러 음악가가 동시에 각기 다른 음을 연주하는 것과 같습니다. 각 음악가는 서로 다른 음표(상태)를 연주하고, 양자 게이트는 이 음들이 서로 간섭하도록 조율합니다. 우리가 원하는 멜로디(정답)는 보강 간섭으로 더 크게 들리도록, 원치 않는 소음(오답)은 상쇄 간섭으로 사라지도록 만듭니다. 마지막에 우리는 가장 크게 들리는 멜로디(높은 확률의 상태)를 측정하여 결과로 얻게 됩니다.
이런 방식의 계산이 강력한 이유는 고전 컴퓨터는 각 상태를 하나씩 순차적으로 계산해야 하지만, 양자 컴퓨터는 모든 상태를 동시에 처리할 수 있기 때문입니다. 문제의 크기가 커질수록 이 차이는 극적으로 커집니다.
결론적으로, 양자 계산은 단순히 더 빠른 계산이 아니라, 양자의 특성 중 파동의 원리를 이용한 완전히 새로운 계산 패러다임입니다. 파동의 간섭 현상을 통해 원하는 답을 찾아가는 이 방식은 궁극적으로 기존 컴퓨터로는 해결하기 어려운 복잡한 문제들을 효율적으로 풀 수 있게 됩니다. 따라서 원하는 결과값이 나올 수 있도록 양자 회로를 설계하는 것이 무엇보다 중요합니다.
표4에서 양자 연산에 이용되는 양자 중첩, 얽힘, 간섭의 차이를 설명하며 이번 블로그를 마치도록 하겠습니다.
| 구분 | 정의 및 특징 | 대표적 예시, 의미 | 양자 컴퓨팅에서의 역할 |
|---|---|---|---|
| 양자 중첩 |
|
|
|
| 양자 얽힘 |
|
|
|
| 양자 간섭 |
|
|
|
<표4. 양자 연산에서 사용되는 양자 중첩, 얽힘, 간섭의 차이>
맺음말
이번 블로그에서는 양자 컴퓨팅의 핵심 개념인 큐비트와 양자 회로에 대해 살펴보았습니다. 양자 컴퓨터가 빠르다는 것은 단순히 개별 연산 속도가 빠르다는 의미가 아니라, 양자 중첩과 얽힘을 통해 문제의 크기가 커질수록 총계산 횟수를 획기적으로 줄일 수 있다는 점에 있습니다.
양자 회로는 큐비트를 조작하여 양자 연산을 수행하는 핵심 구조로, 여러 양자 게이트를 시간 순서대로 배열한 설계도입니다. 고전 컴퓨터의 논리 회로와 달리, 양자 회로는 가역성을 가지며 정보 손실이 없어 에너지 소비가 적다는 특징이 있습니다.
양자 연산의 원리는 파동과 간섭 현상에 기반합니다. 양자 컴퓨터는 설계된 양자 회로에 따라 파동의 보강 간섭과 상쇄 간섭을 활용하여 정답에 해당하는 상태의 확률 진폭을 증가시키고, 오답에 해당하는 상태의 확률 진폭은 제거하는 방식으로 작동합니다. 이러한 방식으로 양자 컴퓨터는 모든 가능한 상태를 동시에 처리할 수 있어, 문제의 크기가 커질수록 고전 컴퓨터와의 성능 차이가 극대화됩니다.
다음 블로그에서는 양자 컴퓨팅의 핵심 요소인 QPU와 다양한 양자 하드웨어 플랫폼에 대해 알아보겠습니다.