Simulating Fluid Mechanics using Quantum Computing on Amazon Braket with Haiqu and Quanscient

Numerical simulations of complex fluid dynamics, electromagnetics and thermomechanical problems are crucial in the automotive and aerospace industries for designing and optimizing components like airplane wings, yet modeling continuum physics on high-resolution grids pushes classical computing to its limits. Quantum computing offers a potential path to overcome these barriers by encoding large simulation grids with fewer computational resources and potentially accelerating numerical solvers.

However, since these quantum applications require the execution of deep circuits beyond the coherence times available on today’s hardware, they are often considered impractical in the immediate future. As finalists in the Airbus and BMW Quantum Mobility Challenge in 2024, a joint team from Haiqu and Quanscient showed that solving these difficult problems may be possible sooner than expected. Today, we explore in more detail how the team approached the challenge.

The team demonstrated the execution of various quantum Computational Fluid Dynamics (CFD) algorithms on currently available trapped ion devices. This was enabled by Haiqu’s application-agnostic execution and error-mitigation tools combined with tailored algorithmic developments by Haiqu researchers, and Quantum Lattice Boltzmann Method (QLBM) algorithms provided by Quanscient. Together, we achieved results surpassing those previously reported in the literature, advancing the state of the art towards solving industrial-scale CFD problems of practical value on quantum computers.

Amazon Braket and AWS cloud infrastructure helped us to achieve these outcomes. Quanscient used Braket as a testbench for studying the simulated QPU execution of subroutines in the QLBM circuits, while Haiqu’s middleware utilized AWS to orchestrate distributed classical processing and simulated QPUs via services like Amazon SageMaker and Amazon CloudWatch.

Integration with Braket also provides convenient access to state-of-the-art quantum hardware, like the IonQ devices. In this post, we’ll highlight in more detail the methodology used by Haiqu and Quanscient in solving CFD problems using quantum simulators and IonQ hardware on Amazon Braket.

Solving Fluid Mechanics Problems using Quantum Algorithms

The increasing industrial need for higher space-time resolutions, resulting in growth of the computational complexity of partial differential equation (PDE) simulations, is a bottleneck in e.g., aerodynamics CFD simulations. Various quantum-aided approaches have been proposed, where the whole or parts of the calculation are performed on a quantum computer to achieve speedups. While some approaches use only a few qubits, fitting on near-term QPUs, the depth of the resulting circuits still limits the immediate applicability of such methods and prevents utility applications [1,2,3]. Consequently, demonstrations were limited to simulated results or small toy models executed on a very small scale (3 to 6 qubits) [1].

To accurately execute deep quantum circuits and bring forward the prospect of running viable CFD simulations, the team from Haiqu and Quanscient used Haiqu’s quantum middleware software stack and tailored quantum applications subroutines. We developed, implemented, and executed — on real and simulated noisy devices from IonQ — CFD calculations related to air flow simulations (fluid advection-diffusion).

The team used the Quantum Lattice Boltzmann Method (QLBM) to map the classical partial differential equations (PDEs) to a quantum computation. The QLBM approaches developed by Quanscient offer a path to simulating more complex equations and boundary conditions than currently possible with Hamiltonian methods. The hybrid quantum-classical loop requires the quantum circuit for just a single time step to be executed on the QPU, and Haiqu tailored their middleware tools to enhance all the major components of the QLBM simulation and enable running the required deep circuits. For the first time, this allowed the execution of three steps of QLBM time evolution on a record 64×64 spatial grid using just 16 qubits on the IonQ Aria 1 quantum device accessed via Amazon Braket. By running a noiseless quantum simulator for the full NACA0012 airfoil computation requiring 23 qubits for a 256×256 spatial grid, Quanscient also demonstrated the potential near-term viability of QLBM simulations for industrially relevant benchmarks.

Simulating Fluid Advection-Diffusion using Quantum Lattice Boltzmann Methods with Amazon Braket

The Lattice Boltzmann Method (LBM) is a numerical approach for solving the Navier–Stokes equations by directly simulating macroscopic scalar quantities such as fluid density on a discrete lattice, whose points (lattice sites) make up the computational grid. In LBM, the DnQm lattice configuration has n dimensions, and each lattice site is connected to m neighboring sites with discrete lattice velocity vectors – see Figure 1.

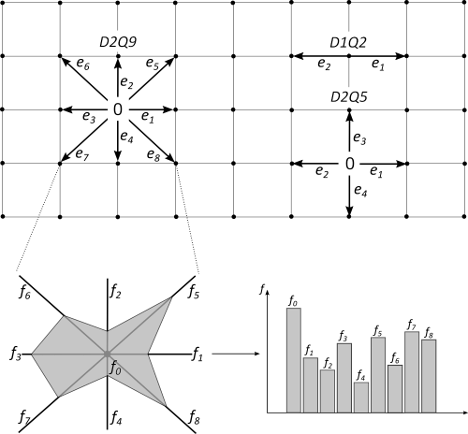
Figure 1: Examples of DnQm lattice configurations for the LBM, with n dimensions and m speeds. The top figure shows examples for D1Q2, D2Q5 and D2Q9, and the bottom figure highlights the number of particles fi moving with speed ei.

The Quantum Lattice Boltzmann Method (QLBM) offloads some of the computationally expensive aspects of LBM onto a quantum processing unit (QPU) [4]. The primary advantages of the QLBM over its classical counterpart include the logarithmic scaling of the number of qubits required to represent the lattice with the size of the lattice and the parallel execution of the propagation step through quantum superposition enabling logarithmic growth in the quantum gate requirement per time step with increasing lattice size.

The QLBM algorithm is based on the lattice Boltzmann equation

where f_α is the particle distribution function along the α link, f_α^eq is the local equilibrium distribution function, e_α is the particle velocity vector, S is the force (source) term, w_α is the weighting factor in the direction α, t is time, Δt is the time step, and ε = Δt/τ, where τ is the single relaxation time.

Two-dimensional non-isothermal incompressible flow can be simulated by solving the Navier-Stokes (NS) equations coupled with the energy equation in the form of the advection-diffusion equation (ADE), where the simplification of the governing NS equations with the vorticity ω and stream function ψ as dependent variables is introduced as

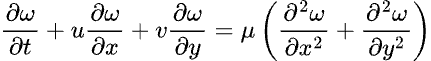
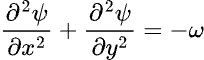
where x, y are the Cartesian coordinates, u(x,y), v(x,y) are velocities, is the fluid density, and μ is the dynamic viscosity. The energy equation can be written as

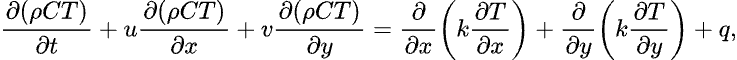
where T(x,y) is the temperature, q(x,y) represents heat source per unit volume, while ρ, C and k are density, specific heat and thermal conductivity of the medium, respectively.

To solve the stream-vorticity equations coupled with the energy equation using the lattice Boltzmann method (LBM), the simple D2Q5 lattice configuration is used. In the case of the vorticity and energy equation, the corresponding equilibrium distribution function is formulated as

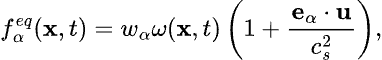
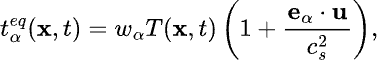
where u = ui + vj (i and j are unit vectors along the x and y directions) and c_s is speed of sound.

For the stream function equation, where only the diffusion part is present, the equilibrium distribution function takes the much simpler form

By taking the parameter ε = 1 in the LBM equation the propagation step takes the form

At the end of each time step, the macroscopic variables for vorticity ω(x, t), stream function ψ(x, t) and temperature T(x, t) are calculated as

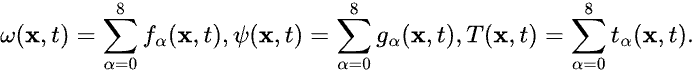
In the quantum setting, vorticity, stream function, and temperature are encoded in a quantum state, and a QLBM circuit is constructed to implement the collision and propagation terms updating the distributions. Quanscient and Haiqu devised an improved hybrid QLBM algorithm that incorporated Haiqu’s tools such as subcircuit compression, state preparation [6] and error mitigation routines. This is schematically shown in Figure 2.

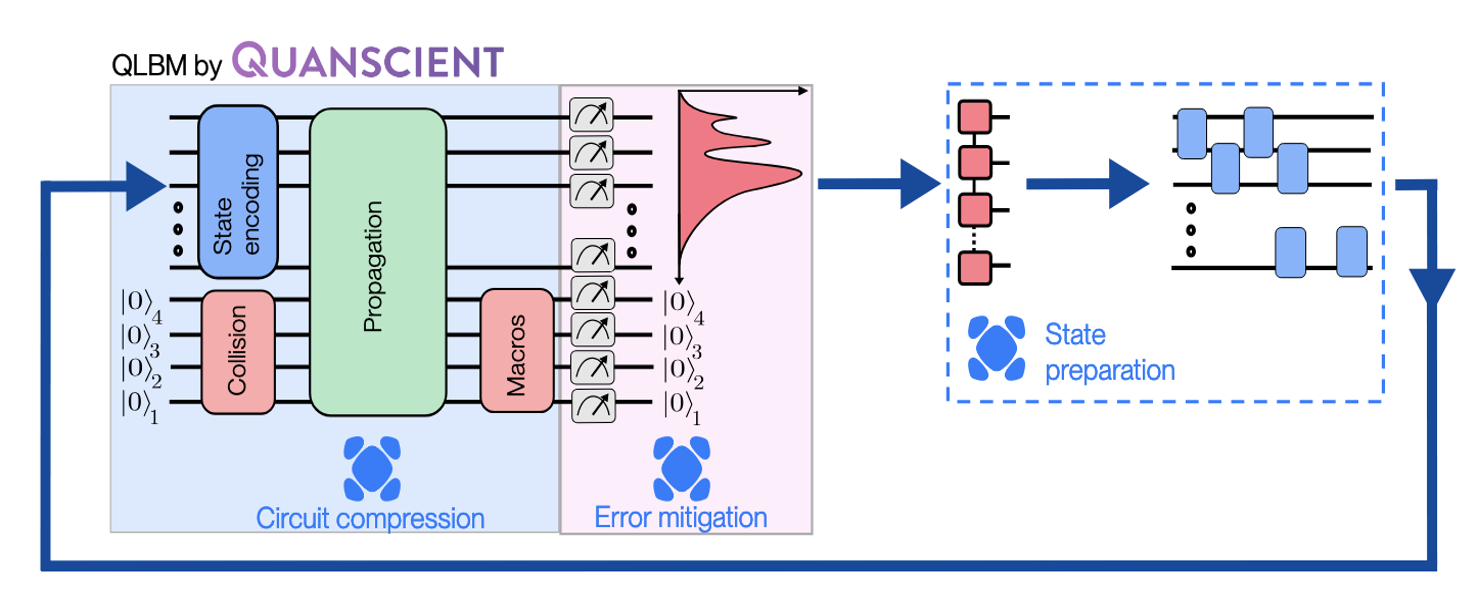
Figure 2 – The optimized hybrid QLBM algorithm, featuring subcircuit compression, state preparation, and lightweight error mitigation.

The above innovations allowed Haiqu and Quanscient to execute, for the first time, several iterations of the full QLBM loop on the IonQ Aria 1 QPU accessed via Amazon Braket. Using Haiqu’s middleware, we were able to perform three steps of evolution for the two-dimensional advection-diffusion equation (ADE) [5] on lattices as large as 64×64 and involving up to 16 qubits. The number of steps executed is limited by the error rates of the current devices, which we expect to improve in upcoming generations.

Each circuit was constructed from two parts (the state encoding portion and the main circuit provided by Quanscient) and pre-processed using Haiqu’s proprietary technology, and then submitted to the QPU via the Amazon Braket SDK (BDK). After receiving the measurement outcomes from the BDK, the time-evolved state was extracted by post-selecting on the state of the auxiliary qubits. This process was repeated for each QLBM step for the ADE problem.

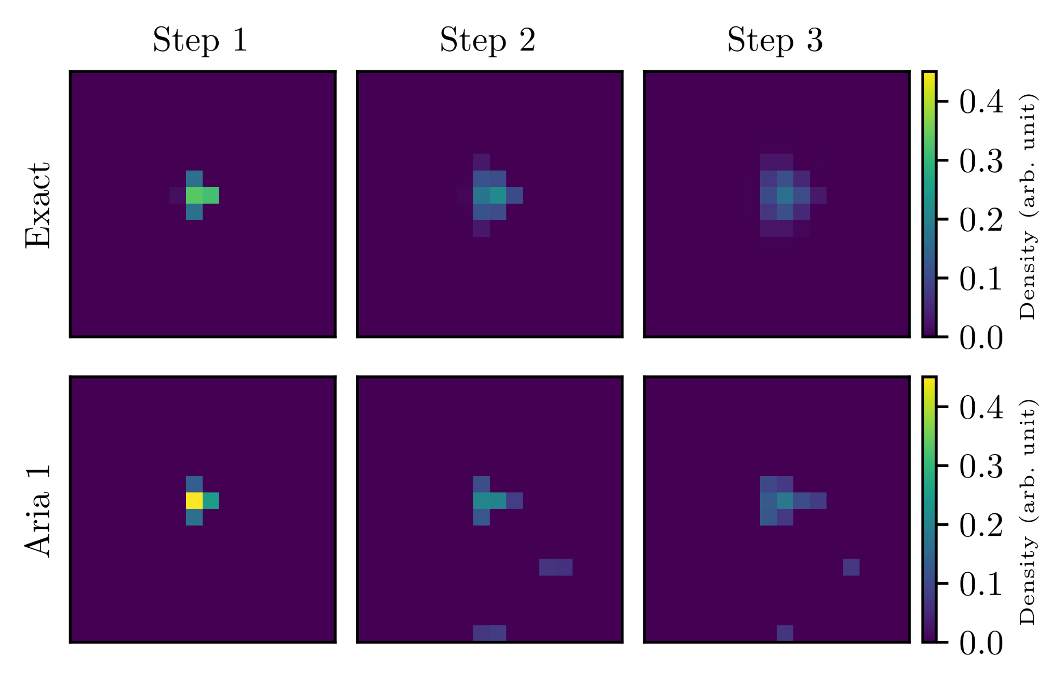
Figure 3 – Three steps of QLBM evolution for the ADE on the IonQ Aria 1 QPU with Haiqu middleware (bottom) and on an ideal state vector simulator (top). Here a 16 × 16 lattice (12-qubit circuit) was used.

Shown graphically in Figure 3 for the 12-qubit case, these results are the first end-to-end execution of multiple QLBM steps on quantum hardware. The original QLBM circuit on the IonQ Aria 1 was 802 gates deep and, despite this very large depth, the QPU results obtained using Haiqu’s middleware (in particular, approximate subcircuit compilation and lightweight noise mitigation) closely resemble the exact simulation results. This agreement can be viewed quantitatively in Figure 4.

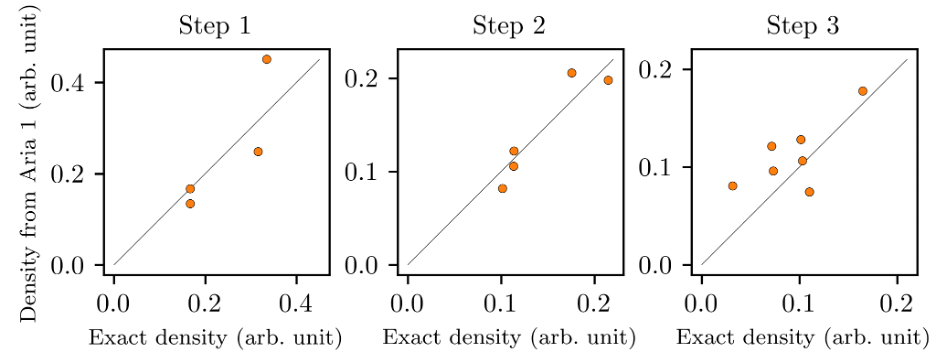
Figure 4 – Quantitative comparison between results obtained for the first three steps of 12-qubit QLBM execution on IonQ Aria 1 (vertical axis) and the exact values (horizontal axis). Deviations from the diagonal line are due primarily to device noise.

Scaling this method to a 64×64 grid and 16 qubits underscores the potential of quantum computing to address realistic CFD applications and emphasizes the necessity of concerted efforts in improving higher-level algorithms and practical quantum middleware engineering. To make this point explicit, Quanscient performed full QLBM simulations of a practical aerodynamic benchmark on an ideal noiseless quantum simulator. Here just 23 qubits were sufficient to simulate the airflow around a NACA0012 airfoil coupled with temperature transport on a 256×256 lattice for 25,000 steps, as shown in Figure 5. While this is currently out of the reach of QPUs as the present Navier-Stokes algorithm results in relatively deep circuits for today’s devices, it demonstrates the near-term capability of quantum approaches as devices continue to improve.

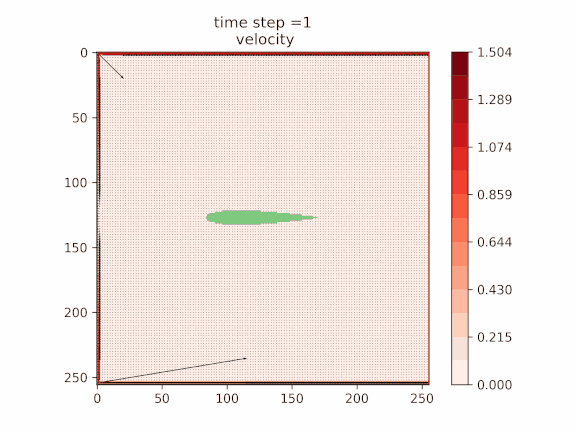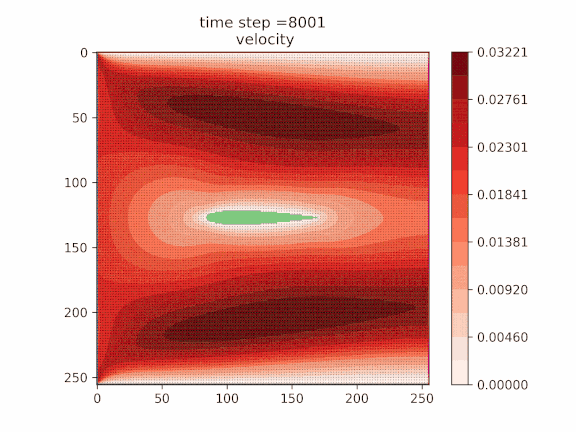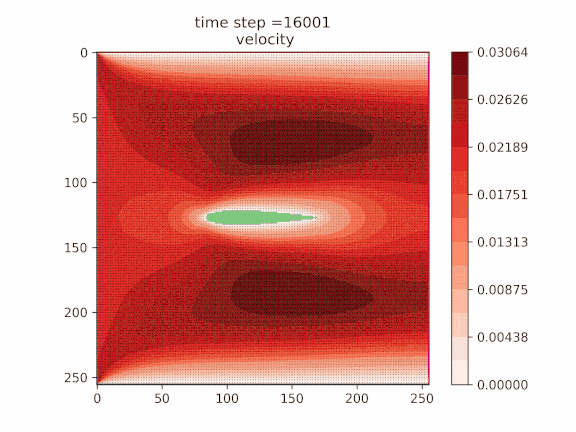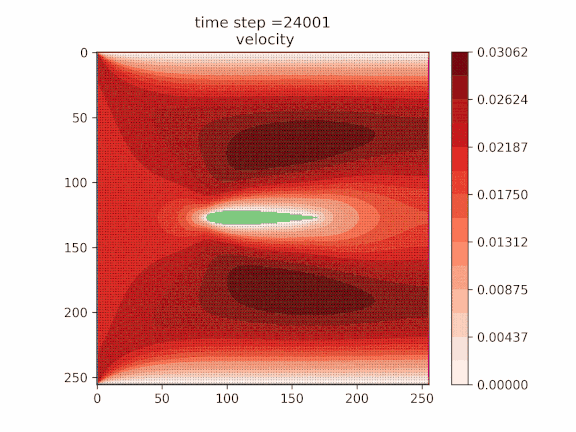
Figure 5 – Velocity, temperature, and stream-function fields around the NACA0012 airfoil up to 25,000 steps of QLBM obtained by Quanscient on an ideal simulator. The temperature, stream, and velocity are given here in the LBM units, which are LBM-specific computational units [Succi].

Conclusions

We have discussed how quantum computing may be applied to computational fluid dynamics problems, and the potential to address real-world engineering challenges in aerospace and automotive industries. We highlighted the crucial synergy between domain-specific algorithm development, as pursued by Quanscient, the tailored quantum middleware and execution tools developed by Haiqu, and the computational infrastructure provided by AWS . Such collaborations will be instrumental in delivering meaningful computational advantage with quantum computers.

With the specific methods presented here, an advantage over classical computing methods may be possible in the future in simulations of airplane design containing on the order of 100 qubits enabling simulation of beyond 1000 billion grid points. Currently, some quantum computers deliver the qubit numbers required but cannot execute large numbers of algorithmic operations with high fidelity. Quanscient’s QLBM exhibits logarithmic scaling of operations with the size of the problem, yielding an algorithmic advantage in speed and scale over classical methods. At the utility level, the measure-re-encode loop for time-stepping used in the present work becomes infeasible, and hence, to simulate multiple time steps and thus a meaningful physics problem, we would need to be able to execute some thousands of quantum gates with high fidelity, which is where Haiqu’s approaches become particularly useful. Haiqu’s middleware solutions and Quanscient’s algorithms hold a strong near-to-medium-term promise in the field of quantum computational fluid dynamics.

To learn more about Amazon Braket and quantum computing on AWS, visit the Amazon Braket homepage or reach out to the Amazon Advanced Solutions Lab.

For further details about Haiqu’s middleware technology and Quanscient’s quantum simulation algorithms reach out to mykola@haiqu.ai and valtteri.lahtinen@quanscient.com respectively.

References

[1] Yuki Sato, Ruho Kondo, Ikko Hamamura, Tamiya Onodera, and Naoki Yamamoto. “Hamiltonian simulation for time-evolving partial differential equation by scalable quantum circuits”, arXiv:2402.18398, (2024).

[2] Shi Jin, Nana Liu, and Yue Yu. “Quantum simulation of partial differential equations via Schrödingerisation: Technical details”, arXiv:2212.14703, (2022).

[3] Antonio David Bastida Zamora, Ljubomir Budinski, Ossi Niemimäki, and Valtteri Lahtinen. “Efficient quantum lattice gas automata”, arXiv:2402.16488, (2024).

[4] Budinski, Ljubomir. “Quantum algorithm for the Navier–Stokes equations by using the streamfunction-vorticity formulation and the lattice Boltzmann method”, International Journal of Quantum Information, 20(02):2150039, (2022). doi:10.1142/S0219749921500398

[5] Budinski, Ljubomir. “Quantum algorithm for the advection–diffusion equation simulated with the lattice Boltzmann method”, Quantum Information Processing, 20(2), (2021). doi:10.1007/s11128-021-02996-3

[6] Vladyslav Bohun, Illia Lukin, Mykola Luhanko, Georgios Korpas, Philippe J.S. De Brouwer, Mykola Maksymenko and Maciej Koch-Janusz. “Scalable and shallow quantum circuits encoding probability distributions informed by asymptotic entanglement analysis”, arXiv:2412.05202, (2024)

[Succi] Succi, S. The Lattice Boltzmann Equation: For Fluid Dynamics and Beyond; Oxford University Press: Oxford, UK, 2001